/* 404CTF */

404CTF Writeup - Hardware Security

Jun 20, 2023 · 10 min read

Un courier suspect

This challenge is a short introduction to hardware security, and in particular to Logisim software for creating and simulating electronic circuits.

The challenge is fairly simple and is divided into 4 parts

Part 1

La première nous donne directement un morceau du flag : 404CTF{L3_:

Part 2

The second part introduces us to a multiplexer (an electronic component that allows us to choose between several inputs). By clicking on the clock a number of times long enough to loop, we obtain the following code: 4d 30 6d 33 6e 54 5f 33 53 74 5f 56 33 6e 55 5f:

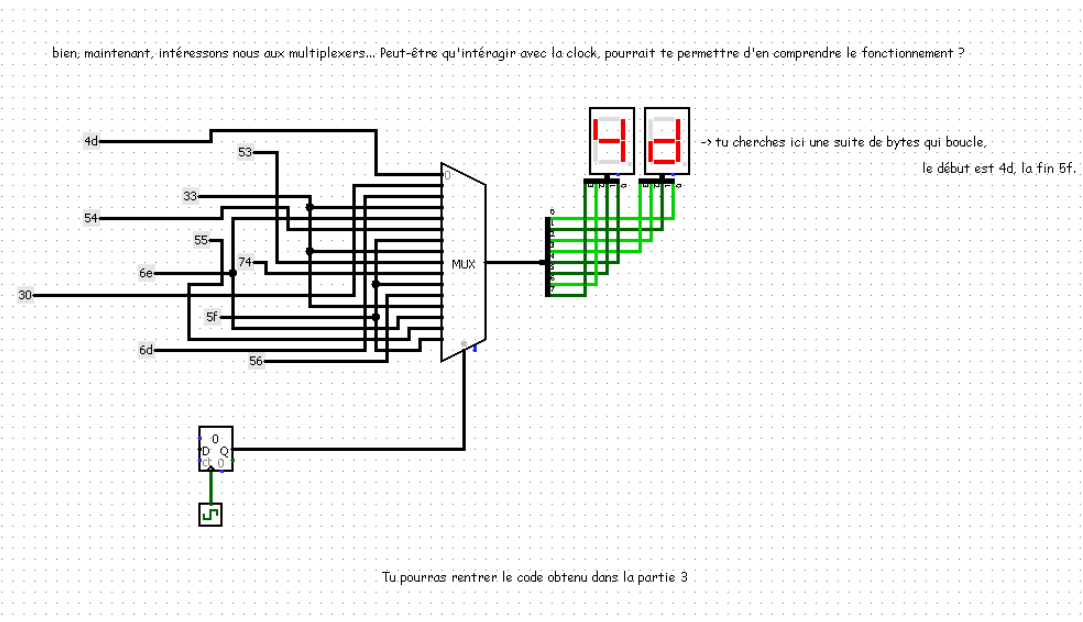
Part 3

In part 3, we enter the previous hex code in a block to produce a text. By entering the code obtained in part 2, we obtain another part of the flag: M0m3nT_3St_V3nU_:

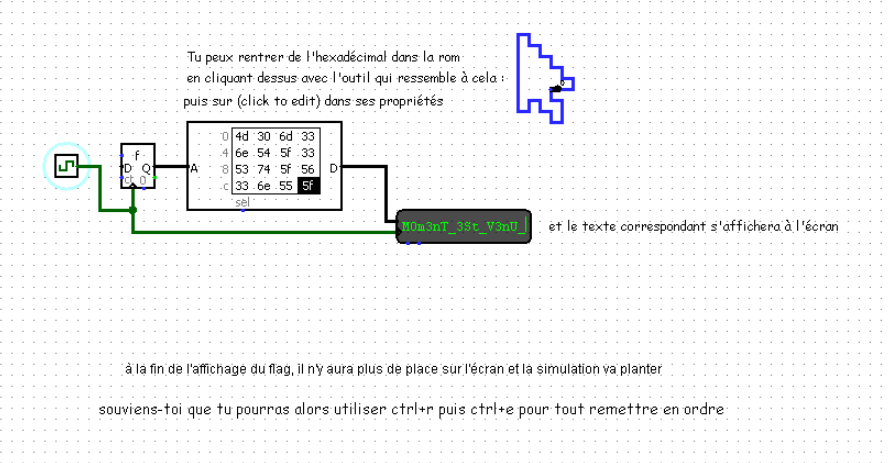
Part 4

Part 4 also features a multiplexer, but it doesn’t seem to work. In fact, after the multiplexer is a blackbox, consisting only of an AND gate between 0 and the multiplexer output. The problem is x & 0 = 0 for whatever x, we’re instead interested of x. We can achieve this by swapping the 0 with ff. Which gives us a new code: 44 33 5f 35 34 6d 75 73 33 72 7d 00, which we can put in component part 3 to get the last part of flag D3_54mus3r}.

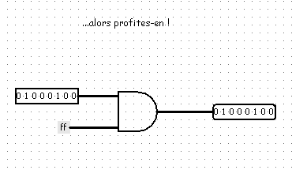
Concatenating these parts gives us the flag: 404CTF{L3_M0m3nT_3St_V3nU_D3_54mus3r}.

À la trace

In this challenge, we have to decrypt a message encrypted by an electronic device for which we have an operating trace for a string of characters. The flag is the string that generates this hexadecimal sequence:

49 b7 71 9f 90 cc 74 9f ca a4 64 b9 83 7a 9e 5e`

The challenge gives us the wave forms in .vcd format due to the input: I_want_my_coffee. I used GTKWave to view the wave forms and here is the result:

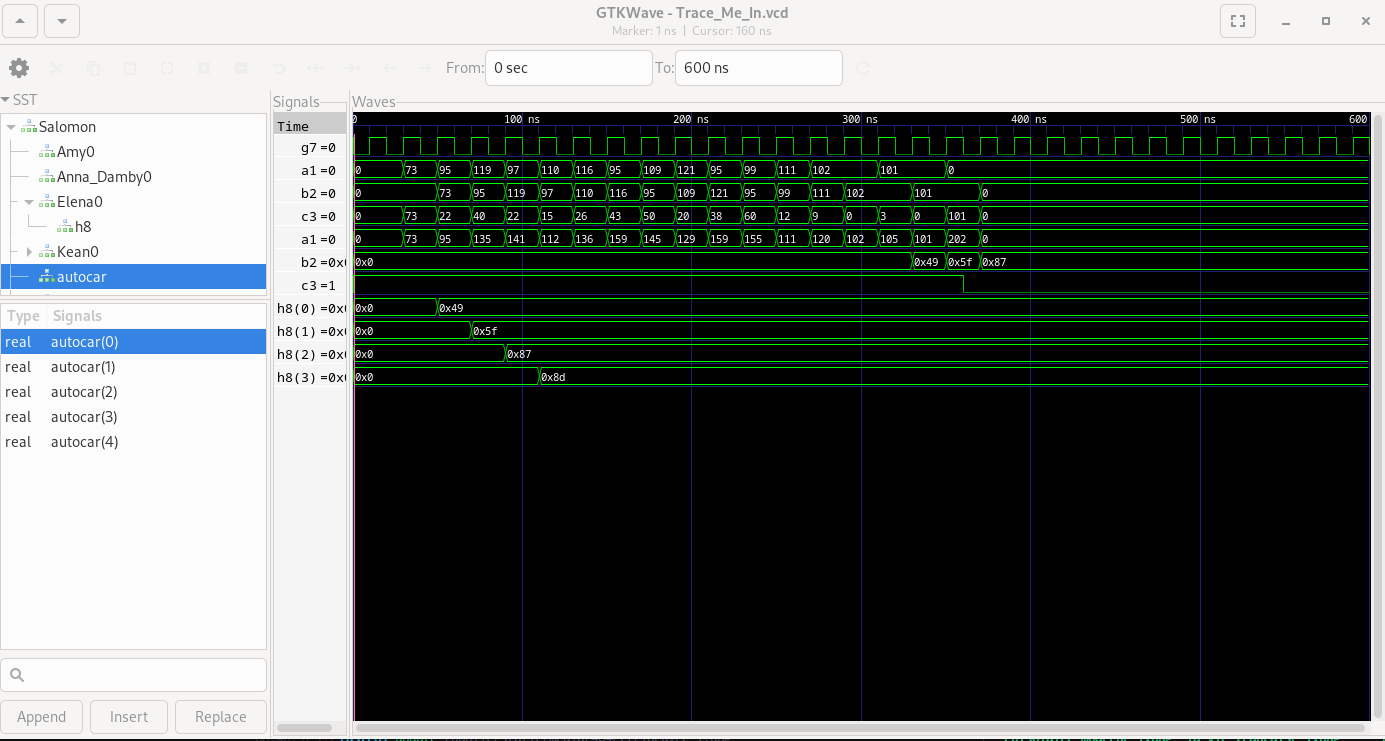
From the wave, we can read the output sequence corresponding to this input. The idea is the reverse the transformation done by the circuit in order to get the flag.

Analyzing the circuit

Looking at the Amy0 module, we notice that:

Amy0.a1 represents the input sequence.
Amy0.b2 represents the same sequence delayed by one cycle, 0 used as a padding
Amy0.c3 represents Amy.a1 ^ Amy.b2

The relevant signals in the Elena0 module are:

Elena0.a1 which represents Amy.a1 + Amy.c3
Elena0.b2 which stays 0 until the input ends (count the number of character) and then starts playing a hex sequence 49 5f 87 ..
Elena0.c1 which represent whetever this password is correct or not, since 49 is the same as the first character of the encoded password, it stays up but then goes low when we meet 5f != b7

These elements allow us to deduce that the ouput sequence verifies output[i] = input[i-1] + (input[i] ^ input[i-1]) for i >= 1 and output[0] = input[0].

Reversing this is a piece of cake:

encoded_password = [0x49, 0xb7, 0x71, 0x9f, 0x90, 0xcc, 0x74, 0x9f, 0xca, 0xa4, 0x64, 0xb9, 0x83, 0x7a, 0x9e, 0x5e]
password = [encoded_password[0]]

for i in range(1, len(encoded_password)):
  password.append(
    (encoded_password[i] - password[i-1]) ^ password[i-1]
  )


flag = "".join(chr(c) for c in password)
print(f"404CTF{{{flag}}}")

Running this script yields the flag: 404CTF{I'm_n0t_4Dd1ct^^}

Un réveil difficile

In this challenge, we have a Logisim file consisting of a main module and a blackbox. The operation is quite simple: we have a counter that selects an input for 2 multiplexers, which generate a 16-bit output each. The two outputs are concatenated into a 32-bit number, itself encrypted by the blackbox before being displayed on 4 7-segment displays.

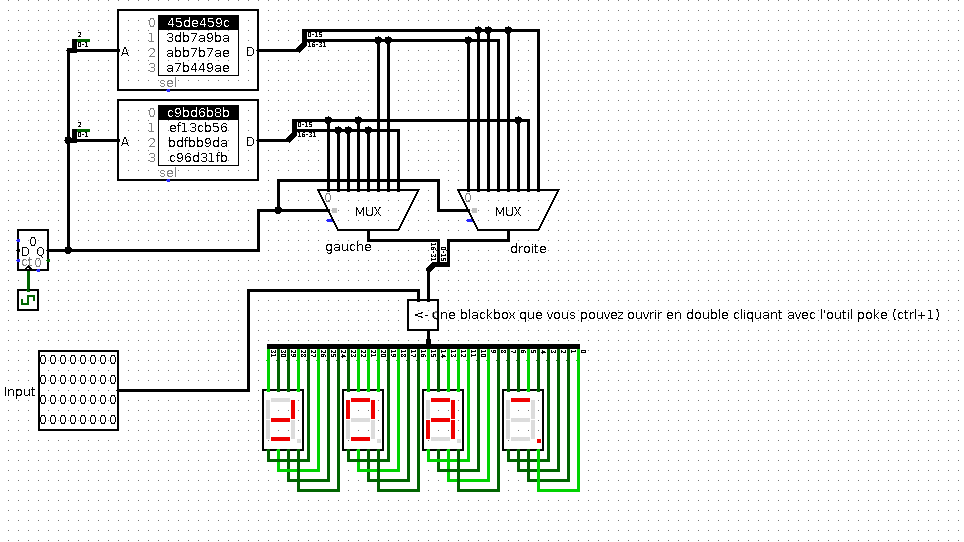
On the left, you can see the blackbox’s second input, a 32-bit number corresponding to an encryption key. From the challenge statement, we know that the first letters of the flag are Un_c, we can bruteforce the encryption key character by character (32bit clicks max for each) and that should do.

Another solution is the reverse the blackbox. It looks complicated but there is some structure to it:

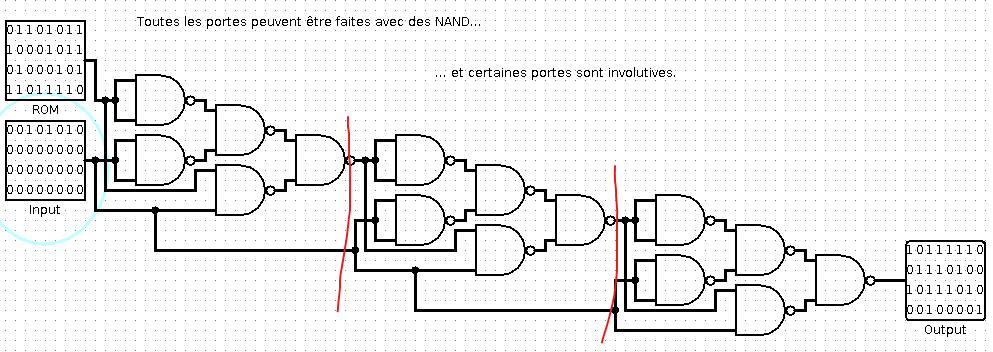
It has three stages, each stage transforms (input[i], key[i]) -> (input[i] ^ key[i], key[i]) and in the last stage key[i] is discarded. In the end, the result is a simple xor operation. Since we know the first part of the flag, the key is easily determined.

The flag is: 404CTF{Un_cH1FFrA9e_A55e2_bi3n_d3PreCie}.

L’Être ou le néant

In this challenge, we’ll be analyzing a Python file using the myhdl library. This library can be used to produce code similar to HDL (Hardware Description Language) and execute it with a Python interpreter.

HDL is a programming language used to describe the behavior of electronic components. Unlike a “traditional” compiled language, which produces machine-language code, an HDL produces the equivalent of an electronic schematic. The code is excuted in parralel as you would expect from a HDL simulator.

from myhdl import *

@block
def AND(a, b, z):
    @always_comb
    def core():
        z.next = a & b

    return core

@block
def OR(a, b, z):
    @always_comb
    def core():
        z.next = a | b

    return core

@block
def XOR(a, b, z):
    @always_comb
    def core():
        z.next = a ^ b

    return core

@block
def NOT(a, z):
    @always_comb
    def core():
        z.next = not a

    return core


@block
def Block7(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(51)]
    F0 = XOR(b[9], b[16], t[0])
    F1 = OR(b[0], t[0], t[1])
    F2 = AND(b[14], b[15], t[2])
    F3 = NOT(t[2], t[3])
    F4 = AND(b[5], t[3], t[4])
    F5 = AND(b[7], b[11], t[5])
    F6 = AND(t[4], t[5], t[6])
    F7 = NOT(t[6], t[7])
    F8 = XOR(b[3], t[7], t[8])
    F9 = AND(b[4], b[8], t[9])
    F10 = OR(t[8], t[9], t[10])
    F11 = NOT(t[10], t[11])
    F12 = XOR(t[1], t[11], t[12])
    F13 = OR(b[10], b[2], t[13])
    F14 = OR(t[13], b[13], t[14])
    F15 = OR(b[8], b[2], t[15])
    F16 = OR(b[12], b[5], t[16])
    F17 = OR(t[16], b[12], t[17])
    F18 = OR(t[15], t[17], t[18])
    F19 = OR(t[14], t[18], t[19])
    F20 = NOT(t[19], t[20])
    F21 = OR(t[12], t[20], t[21])
    F22 = NOT(t[21], t[22])
    F23 = OR(b[14], b[4], t[23])
    F24 = OR(b[7], b[1], t[24])
    F25 = OR(t[23], t[24], t[25])
    F26 = OR(b[16], b[3], t[26])
    F27 = OR(b[15], b[0], t[27])
    F28 = OR(t[26], t[27], t[28])
    F29 = OR(t[25], t[28], t[29])
    F30 = OR(b[9], b[6], t[30])
    F31 = OR(b[13], b[1], t[31])
    F32 = OR(b[11], t[31], t[32])
    F33 = OR(t[30], t[32], t[33])
    F34 = OR(t[29], t[33], t[34])
    F35 = OR(b[13], b[0], t[35])
    F36 = OR(b[15], b[4], t[36])
    F37 = OR(b[6], t[36], t[37])
    F38 = OR(b[16], b[1], t[38])
    F39 = OR(t[37], t[38], t[39])
    F40 = OR(t[39], b[6], t[40])
    F41 = OR(t[35], t[40], t[41])
    F42 = OR(b[11], b[3], t[42])
    F43 = OR(b[7], t[42], t[43])
    F44 = OR(b[14], b[10], t[44])
    F45 = OR(b[9], t[44], t[45])
    F46 = OR(t[43], t[45], t[46])
    F47 = OR(t[41], t[46], t[47])
    F48 = AND(t[34], t[47], t[48])
    F49 = OR(t[22], t[48], t[49])
    F50 = NOT(t[49], t[50])

    @always_comb
    def core():
        z.next = t[50]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50


@block
def Block6(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(88)]
    F0 = NOT(b[10], t[0])
    F1 = NOT(b[16], t[1])
    F2 = NOT(b[6], t[2])
    F3 = AND(t[1], t[2], t[3])
    F4 = AND(t[0], t[3], t[4])
    F5 = NOT(b[8], t[5])
    F6 = AND(t[5], b[3], t[6])
    F7 = AND(t[4], t[6], t[7])
    F8 = NOT(b[4], t[8])
    F9 = NOT(b[13], t[9])
    F10 = AND(b[15], t[9], t[10])
    F11 = NOT(b[7], t[11])
    F12 = AND(t[10], t[11], t[12])
    F13 = AND(b[12], b[0], t[13])
    F14 = AND(t[12], t[13], t[14])
    F15 = AND(t[8], t[14], t[15])
    F16 = AND(t[7], t[15], t[16])
    F17 = NOT(b[3], t[17])
    F18 = OR(b[4], t[17], t[18])
    F19 = NOT(b[0], t[19])
    F20 = OR(b[8], t[19], t[20])
    F21 = OR(t[18], t[20], t[21])
    F22 = OR(b[13], b[7], t[22])
    F23 = OR(b[10], t[22], t[23])
    F24 = OR(t[23], b[8], t[24])
    F25 = OR(t[21], t[24], t[25])
    F26 = NOT(b[12], t[26])
    F27 = OR(b[16], t[26], t[27])
    F28 = OR(t[27], b[6], t[28])
    F29 = NOT(b[15], t[29])
    F30 = OR(t[29], b[10], t[30])
    F31 = OR(t[28], t[30], t[31])
    F32 = OR(t[25], t[31], t[32])
    F33 = NOT(t[32], t[33])
    F34 = OR(t[16], t[33], t[34])
    F35 = NOT(t[34], t[35])
    F36 = NOT(b[3], t[36])
    F37 = OR(b[8], t[36], t[37])
    F38 = OR(b[6], b[4], t[38])
    F39 = NOT(b[15], t[39])
    F40 = OR(t[39], b[7], t[40])
    F41 = NOT(b[12], t[41])
    F42 = NOT(b[0], t[42])
    F43 = OR(t[41], t[42], t[43])
    F44 = OR(t[40], t[43], t[44])
    F45 = OR(t[38], t[44], t[45])
    F46 = OR(t[37], t[45], t[46])
    F47 = OR(b[16], b[10], t[47])
    F48 = OR(b[13], b[5], t[48])
    F49 = OR(t[47], t[48], t[49])
    F50 = OR(t[46], t[49], t[50])
    F51 = AND(t[35], t[50], t[51])
    F52 = NOT(t[51], t[52])
    F53 = NOT(b[2], t[53])
    F54 = AND(t[53], b[1], t[54])
    F55 = XOR(b[13], b[14], t[55])
    F56 = OR(t[54], t[55], t[56])
    F57 = NOT(b[11], t[57])
    F58 = NOT(b[9], t[58])
    F59 = OR(t[57], t[58], t[59])
    F60 = OR(t[59], b[6], t[60])
    F61 = NOT(b[9], t[61])
    F62 = NOT(b[11], t[62])
    F63 = OR(t[62], b[7], t[63])
    F64 = OR(t[61], t[63], t[64])
    F65 = AND(t[60], t[64], t[65])
    F66 = NOT(t[65], t[66])
    F67 = AND(t[56], t[66], t[67])
    F68 = NOT(t[67], t[68])
    F69 = XOR(b[4], b[9], t[69])
    F70 = AND(b[3], t[69], t[70])
    F71 = NOT(t[70], t[71])
    F72 = OR(t[68], t[71], t[72])
    F73 = AND(b[12], b[16], t[73])
    F74 = NOT(t[73], t[74])
    F75 = OR(b[2], t[74], t[75])
    F76 = NOT(t[75], t[76])
    F77 = AND(b[1], b[11], t[77])
    F78 = NOT(b[14], t[78])
    F79 = NOT(b[5], t[79])
    F80 = AND(t[78], t[79], t[80])
    F81 = AND(t[80], b[15], t[81])
    F82 = AND(t[77], t[81], t[82])
    F83 = OR(t[76], t[82], t[83])
    F84 = NOT(t[83], t[84])
    F85 = OR(t[72], t[84], t[85])
    F86 = NOT(t[85], t[86])
    F87 = AND(t[52], t[86], t[87])

    @always_comb
    def core():
        z.next = t[87]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50, F51, F52, F53, F54, F55, F56, F57, F58, F59, F60, F61, F62, F63, F64, F65, F66, F67, F68, F69, F70, F71, F72, F73, F74, F75, F76, F77, F78, F79, F80, F81, F82, F83, F84, F85, F86, F87


@block
def Block5(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(51)]
    F0 = OR(b[10], b[13], t[0])
    F1 = NOT(t[0], t[1])
    F2 = OR(b[14], b[16], t[2])
    F3 = AND(b[12], t[2], t[3])
    F4 = NOT(t[3], t[4])
    F5 = OR(t[1], t[4], t[5])
    F6 = AND(b[5], t[5], t[6])
    F7 = NOT(t[6], t[7])
    F8 = AND(b[7], b[9], t[8])
    F9 = NOT(t[8], t[9])
    F10 = AND(t[7], t[9], t[10])
    F11 = NOT(t[10], t[11])
    F12 = AND(b[0], t[11], t[12])
    F13 = OR(b[4], b[8], t[13])
    F14 = OR(t[13], b[6], t[14])
    F15 = NOT(t[14], t[15])
    F16 = AND(t[12], t[15], t[16])
    F17 = NOT(t[16], t[17])
    F18 = OR(t[17], b[3], t[18])
    F19 = AND(b[11], b[3], t[19])
    F20 = AND(b[4], b[1], t[20])
    F21 = AND(t[19], t[20], t[21])
    F22 = AND(b[13], b[9], t[22])
    F23 = AND(b[14], b[2], t[23])
    F24 = AND(t[22], t[23], t[24])
    F25 = AND(b[7], t[24], t[25])
    F26 = AND(t[21], t[25], t[26])
    F27 = AND(b[4], b[3], t[27])
    F28 = AND(b[13], b[7], t[28])
    F29 = AND(t[28], b[1], t[29])
    F30 = AND(t[27], t[29], t[30])
    F31 = AND(b[14], b[2], t[31])
    F32 = AND(b[11], t[31], t[32])
    F33 = AND(b[9], t[32], t[33])
    F34 = AND(t[33], b[11], t[34])
    F35 = AND(t[30], t[34], t[35])
    F36 = OR(t[26], t[35], t[36])
    F37 = NOT(t[36], t[37])
    F38 = AND(t[18], t[37], t[38])
    F39 = NOT(t[38], t[39])
    F40 = AND(b[12], b[6], t[40])
    F41 = AND(b[10], b[5], t[41])
    F42 = AND(t[40], t[41], t[42])
    F43 = AND(b[8], b[1], t[43])
    F44 = AND(t[42], t[43], t[44])
    F45 = NOT(b[0], t[45])
    F46 = AND(b[16], t[45], t[46])
    F47 = AND(b[15], t[46], t[47])
    F48 = AND(t[47], b[15], t[48])
    F49 = AND(t[44], t[48], t[49])
    F50 = AND(t[39], t[49], t[50])

    @always_comb
    def core():
        z.next = t[50]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50


@block
def Block4(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(53)]
    F0 = OR(b[8], b[15], t[0])
    F1 = NOT(t[0], t[1])
    F2 = AND(b[7], t[1], t[2])
    F3 = NOT(t[2], t[3])
    F4 = OR(b[0], t[3], t[4])
    F5 = NOT(t[4], t[5])
    F6 = NOT(b[12], t[6])
    F7 = AND(t[6], b[4], t[7])
    F8 = AND(t[7], b[13], t[8])
    F9 = NOT(b[0], t[9])
    F10 = AND(b[2], t[9], t[10])
    F11 = NOT(b[5], t[11])
    F12 = AND(t[11], b[14], t[12])
    F13 = AND(t[10], t[12], t[13])
    F14 = OR(b[12], t[13], t[14])
    F15 = NOT(t[14], t[15])
    F16 = XOR(t[8], t[15], t[16])
    F17 = OR(t[5], t[16], t[17])
    F18 = OR(b[2], b[16], t[18])
    F19 = NOT(t[18], t[19])
    F20 = AND(b[3], b[11], t[20])
    F21 = OR(t[19], t[20], t[21])
    F22 = NOT(t[21], t[22])
    F23 = AND(b[15], b[3], t[23])
    F24 = AND(b[15], b[10], t[24])
    F25 = OR(t[23], t[24], t[25])
    F26 = NOT(t[25], t[26])
    F27 = OR(b[6], b[9], t[27])
    F28 = AND(t[26], t[27], t[28])
    F29 = OR(t[28], b[5], t[29])
    F30 = OR(t[22], t[29], t[30])
    F31 = NOT(t[30], t[31])
    F32 = AND(t[17], t[31], t[32])
    F33 = NOT(t[32], t[33])
    F34 = NOT(b[9], t[34])
    F35 = NOT(b[7], t[35])
    F36 = OR(t[34], t[35], t[36])
    F37 = NOT(b[8], t[37])
    F38 = NOT(b[11], t[38])
    F39 = OR(t[38], b[6], t[39])
    F40 = OR(t[37], t[39], t[40])
    F41 = OR(t[36], t[40], t[41])
    F42 = NOT(b[10], t[42])
    F43 = NOT(b[13], t[43])
    F44 = NOT(b[4], t[44])
    F45 = OR(t[43], t[44], t[45])
    F46 = OR(t[42], t[45], t[46])
    F47 = OR(t[41], t[46], t[47])
    F48 = NOT(b[16], t[48])
    F49 = OR(t[48], b[1], t[49])
    F50 = OR(t[47], t[49], t[50])
    F51 = OR(t[33], t[50], t[51])
    F52 = NOT(t[51], t[52])

    @always_comb
    def core():
        z.next = t[52]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50, F51, F52


@block
def Block3(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(43)]
    F0 = OR(b[8], b[0], t[0])
    F1 = OR(b[8], b[13], t[1])
    F2 = AND(t[0], t[1], t[2])
    F3 = OR(b[15], b[8], t[3])
    F4 = OR(b[14], t[3], t[4])
    F5 = OR(b[11], t[4], t[5])
    F6 = OR(b[15], b[14], t[6])
    F7 = OR(t[6], b[11], t[7])
    F8 = OR(t[7], b[9], t[8])
    F9 = AND(t[5], t[8], t[9])
    F10 = OR(t[2], t[9], t[10])
    F11 = OR(b[10], b[14], t[11])
    F12 = NOT(t[11], t[12])
    F13 = OR(b[5], t[12], t[13])
    F14 = AND(t[10], t[13], t[14])
    F15 = NOT(b[16], t[15])
    F16 = OR(t[15], b[0], t[16])
    F17 = OR(b[10], t[16], t[17])
    F18 = NOT(b[1], t[18])
    F19 = OR(t[18], b[4], t[19])
    F20 = OR(t[17], t[19], t[20])
    F21 = OR(b[7], b[6], t[21])
    F22 = OR(t[21], b[11], t[22])
    F23 = OR(b[3], t[22], t[23])
    F24 = OR(t[20], t[23], t[24])
    F25 = OR(t[14], t[24], t[25])
    F26 = NOT(t[25], t[26])
    F27 = NOT(b[2], t[27])
    F28 = AND(b[5], b[1], t[28])
    F29 = AND(t[27], t[28], t[29])
    F30 = OR(b[9], b[2], t[30])
    F31 = OR(t[30], b[12], t[31])
    F32 = OR(b[4], b[7], t[32])
    F33 = AND(t[32], b[16], t[33])
    F34 = OR(t[31], t[33], t[34])
    F35 = OR(b[12], b[6], t[35])
    F36 = OR(b[13], b[15], t[36])
    F37 = OR(t[35], t[36], t[37])
    F38 = OR(t[34], t[37], t[38])
    F39 = NOT(t[38], t[39])
    F40 = OR(t[39], b[3], t[40])
    F41 = AND(t[29], t[40], t[41])
    F42 = AND(t[26], t[41], t[42])

    @always_comb
    def core():
        z.next = t[42]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42


@block
def Block2(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(87)]
    F0 = NOT(b[3], t[0])
    F1 = AND(b[9], t[0], t[1])
    F2 = AND(b[4], b[8], t[2])
    F3 = AND(t[1], t[2], t[3])
    F4 = OR(b[0], t[3], t[4])
    F5 = NOT(b[3], t[5])
    F6 = AND(b[4], b[7], t[6])
    F7 = AND(t[5], t[6], t[7])
    F8 = AND(t[7], b[13], t[8])
    F9 = XOR(b[9], b[10], t[9])
    F10 = AND(t[8], t[9], t[10])
    F11 = OR(t[4], t[10], t[11])
    F12 = OR(b[0], b[6], t[12])
    F13 = XOR(b[12], b[16], t[13])
    F14 = OR(t[13], b[15], t[14])
    F15 = NOT(t[14], t[15])
    F16 = OR(t[12], t[15], t[16])
    F17 = XOR(t[11], t[16], t[17])
    F18 = NOT(b[11], t[18])
    F19 = AND(t[18], b[7], t[19])
    F20 = AND(t[19], b[5], t[20])
    F21 = AND(b[1], t[20], t[21])
    F22 = AND(t[17], t[21], t[22])
    F23 = NOT(t[22], t[23])
    F24 = NOT(b[13], t[24])
    F25 = OR(t[24], b[6], t[25])
    F26 = OR(b[10], t[25], t[26])
    F27 = NOT(b[16], t[27])
    F28 = NOT(b[5], t[28])
    F29 = OR(t[27], t[28], t[29])
    F30 = OR(b[14], t[29], t[30])
    F31 = OR(t[26], t[30], t[31])
    F32 = NOT(b[12], t[32])
    F33 = NOT(b[15], t[33])
    F34 = NOT(b[8], t[34])
    F35 = OR(t[33], t[34], t[35])
    F36 = OR(t[32], t[35], t[36])
    F37 = OR(t[36], b[2], t[37])
    F38 = OR(t[31], t[37], t[38])
    F39 = NOT(b[13], t[39])
    F40 = NOT(b[5], t[40])
    F41 = OR(t[39], t[40], t[41])
    F42 = OR(b[10], t[41], t[42])
    F43 = NOT(b[12], t[43])
    F44 = NOT(b[8], t[44])
    F45 = OR(t[43], t[44], t[45])
    F46 = OR(t[45], b[2], t[46])
    F47 = OR(t[42], t[46], t[47])
    F48 = OR(b[14], b[6], t[48])
    F49 = NOT(b[15], t[49])
    F50 = NOT(b[16], t[50])
    F51 = OR(t[50], b[14], t[51])
    F52 = OR(t[49], t[51], t[52])
    F53 = OR(t[48], t[52], t[53])
    F54 = OR(t[47], t[53], t[54])
    F55 = AND(t[38], t[54], t[55])
    F56 = NOT(t[55], t[56])
    F57 = AND(b[3], b[11], t[57])
    F58 = AND(t[57], b[4], t[58])
    F59 = OR(t[56], t[58], t[59])
    F60 = NOT(t[59], t[60])
    F61 = OR(t[23], t[60], t[61])
    F62 = NOT(t[61], t[62])
    F63 = NOT(b[10], t[63])
    F64 = AND(t[63], b[5], t[64])
    F65 = AND(b[8], b[7], t[65])
    F66 = NOT(b[2], t[66])
    F67 = AND(t[65], t[66], t[67])
    F68 = AND(t[64], t[67], t[68])
    F69 = NOT(b[0], t[69])
    F70 = AND(b[9], t[69], t[70])
    F71 = AND(b[4], t[70], t[71])
    F72 = AND(t[68], t[71], t[72])
    F73 = NOT(b[14], t[73])
    F74 = NOT(b[11], t[74])
    F75 = AND(t[73], t[74], t[75])
    F76 = NOT(b[3], t[76])
    F77 = AND(t[75], t[76], t[77])
    F78 = NOT(b[6], t[78])
    F79 = AND(b[16], t[78], t[79])
    F80 = AND(b[15], t[79], t[80])
    F81 = AND(b[13], t[80], t[81])
    F82 = AND(b[12], b[1], t[82])
    F83 = AND(t[81], t[82], t[83])
    F84 = AND(t[77], t[83], t[84])
    F85 = AND(t[72], t[84], t[85])
    F86 = OR(t[62], t[85], t[86])

    @always_comb
    def core():
        z.next = t[86]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50, F51, F52, F53, F54, F55, F56, F57, F58, F59, F60, F61, F62, F63, F64, F65, F66, F67, F68, F69, F70, F71, F72, F73, F74, F75, F76, F77, F78, F79, F80, F81, F82, F83, F84, F85, F86


@block
def Block1(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(74)]
    F0 = NOT(b[12], t[0])
    F1 = OR(b[15], b[5], t[1])
    F2 = OR(t[0], t[1], t[2])
    F3 = OR(t[2], b[4], t[3])
    F4 = NOT(b[11], t[4])
    F5 = OR(t[4], b[6], t[5])
    F6 = NOT(b[16], t[6])
    F7 = OR(t[6], b[13], t[7])
    F8 = NOT(b[3], t[8])
    F9 = OR(t[7], t[8], t[9])
    F10 = OR(b[9], t[9], t[10])
    F11 = OR(t[5], t[10], t[11])
    F12 = OR(t[3], t[11], t[12])
    F13 = OR(t[12], b[0], t[13])
    F14 = OR(b[11], b[14], t[14])
    F15 = AND(b[8], t[14], t[15])
    F16 = NOT(t[15], t[16])
    F17 = AND(t[13], t[16], t[17])
    F18 = NOT(t[17], t[18])
    F19 = OR(b[2], b[1], t[19])
    F20 = OR(b[10], b[2], t[20])
    F21 = OR(b[8], t[20], t[21])
    F22 = OR(t[19], t[21], t[22])
    F23 = OR(b[10], b[1], t[23])
    F24 = OR(b[2], t[23], t[24])
    F25 = OR(b[8], b[7], t[25])
    F26 = OR(t[24], t[25], t[26])
    F27 = OR(b[10], b[1], t[27])
    F28 = OR(b[8], b[9], t[28])
    F29 = OR(b[2], t[28], t[29])
    F30 = OR(t[27], t[29], t[30])
    F31 = AND(t[26], t[30], t[31])
    F32 = AND(t[22], t[31], t[32])
    F33 = NOT(b[7], t[33])
    F34 = NOT(b[14], t[34])
    F35 = AND(t[34], b[3], t[35])
    F36 = AND(t[33], t[35], t[36])
    F37 = OR(b[13], b[16], t[37])
    F38 = AND(t[37], b[15], t[38])
    F39 = NOT(t[38], t[39])
    F40 = XOR(b[12], t[39], t[40])
    F41 = OR(t[36], t[40], t[41])
    F42 = NOT(t[41], t[42])
    F43 = OR(b[4], b[10], t[43])
    F44 = NOT(t[43], t[44])
    F45 = XOR(t[44], b[6], t[45])
    F46 = AND(t[42], t[45], t[46])
    F47 = OR(t[32], t[46], t[47])
    F48 = NOT(t[47], t[48])
    F49 = AND(t[18], t[48], t[49])
    F50 = NOT(t[49], t[50])
    F51 = OR(b[15], b[9], t[51])
    F52 = OR(t[51], b[0], t[52])
    F53 = NOT(b[16], t[53])
    F54 = NOT(b[3], t[54])
    F55 = OR(t[53], t[54], t[55])
    F56 = OR(b[13], t[55], t[56])
    F57 = OR(b[7], t[56], t[57])
    F58 = OR(b[8], b[1], t[58])
    F59 = OR(b[6], t[58], t[59])
    F60 = OR(t[57], t[59], t[60])
    F61 = OR(t[52], t[60], t[61])
    F62 = NOT(b[11], t[62])
    F63 = OR(t[62], b[5], t[63])
    F64 = NOT(b[12], t[64])
    F65 = OR(t[64], b[10], t[65])
    F66 = OR(b[14], b[2], t[66])
    F67 = OR(t[65], t[66], t[67])
    F68 = OR(t[63], t[67], t[68])
    F69 = OR(b[4], b[5], t[69])
    F70 = OR(t[68], t[69], t[70])
    F71 = OR(t[61], t[70], t[71])
    F72 = AND(t[50], t[71], t[72])
    F73 = NOT(t[72], t[73])

    @always_comb
    def core():
        z.next = t[73]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50, F51, F52, F53, F54, F55, F56, F57, F58, F59, F60, F61, F62, F63, F64, F65, F66, F67, F68, F69, F70, F71, F72, F73


@block
def Block0(a, z):
    b = [Signal(bool(a[i])) for i in range(len(a))]
    t = [Signal(bool(0)) for n in range(56)]
    F0 = NOT(b[8], t[0])
    F1 = AND(t[0], b[4], t[1])
    F2 = NOT(b[13], t[2])
    F3 = NOT(b[1], t[3])
    F4 = AND(t[2], t[3], t[4])
    F5 = AND(t[1], t[4], t[5])
    F6 = NOT(b[9], t[6])
    F7 = NOT(b[3], t[7])
    F8 = AND(t[6], t[7], t[8])
    F9 = NOT(b[5], t[9])
    F10 = NOT(b[2], t[10])
    F11 = AND(t[9], t[10], t[11])
    F12 = AND(t[8], t[11], t[12])
    F13 = NOT(b[15], t[13])
    F14 = NOT(b[12], t[14])
    F15 = AND(t[13], t[14], t[15])
    F16 = AND(t[15], b[0], t[16])
    F17 = AND(t[12], t[16], t[17])
    F18 = AND(t[5], t[17], t[18])
    F19 = AND(b[14], b[15], t[19])
    F20 = NOT(t[19], t[20])
    F21 = AND(b[9], t[20], t[21])
    F22 = OR(b[1], t[21], t[22])
    F23 = NOT(t[22], t[23])
    F24 = AND(b[5], b[7], t[24])
    F25 = NOT(t[24], t[25])
    F26 = AND(b[11], b[16], t[26])
    F27 = NOT(t[26], t[27])
    F28 = OR(b[6], t[27], t[28])
    F29 = NOT(t[28], t[29])
    F30 = XOR(t[25], t[29], t[30])
    F31 = OR(t[23], t[30], t[31])
    F32 = AND(b[0], b[10], t[32])
    F33 = OR(t[32], b[12], t[33])
    F34 = OR(b[2], t[33], t[34])
    F35 = NOT(b[16], t[35])
    F36 = NOT(b[11], t[36])
    F37 = OR(t[35], t[36], t[37])
    F38 = NOT(b[14], t[38])
    F39 = OR(t[38], b[6], t[39])
    F40 = OR(t[37], t[39], t[40])
    F41 = NOT(b[7], t[41])
    F42 = NOT(b[10], t[42])
    F43 = OR(t[42], b[3], t[43])
    F44 = OR(t[41], t[43], t[44])
    F45 = OR(t[40], t[44], t[45])
    F46 = AND(b[8], b[13], t[46])
    F47 = AND(b[4], t[46], t[47])
    F48 = NOT(t[47], t[48])
    F49 = AND(t[45], t[48], t[49])
    F50 = NOT(t[49], t[50])
    F51 = AND(t[34], t[50], t[51])
    F52 = NOT(t[51], t[52])
    F53 = AND(t[31], t[52], t[53])
    F54 = NOT(t[53], t[54])
    F55 = AND(t[18], t[54], t[55])

    @always_comb
    def core():
        z.next = t[55]

    return core, F0, F1, F2, F3, F4, F5, F6, F7, F8, F9, F10, F11, F12, F13, F14, F15, F16, F17, F18, F19, F20, F21, F22, F23, F24, F25, F26, F27, F28, F29, F30, F31, F32, F33, F34, F35, F36, F37, F38, F39, F40, F41, F42, F43, F44, F45, F46, F47, F48, F49, F50, F51, F52, F53, F54, F55


@block
def Tulipe(a, z, sel):

    @always_comb
    def core():
        if sel == 0:
            z.next = a[0]
        elif sel == 1:
            z.next = a[1]
        elif sel == 2:
            z.next = a[2]
        elif sel == 3:
            z.next = a[3]
        elif sel == 4:
            z.next = a[4]
        elif sel == 5:
            z.next = a[5]
        elif sel == 6:
            z.next = a[6]
        elif sel == 7:
            z.next = a[7]

    return core


@block
def plic_ploc(input, output, sel, clk):
    @always(clk.posedge)
    def logic():
        output.next[sel] = input

    return logic

@block
def go_up_go_up_GO_UP(a, clk):
    @always(clk.posedge)
    def seq():
        a.next = a + 1

    return seq

@block
def time_to_see(a, b, clk):
    @always(clk.posedge)
    def core():
        if b == 8:
            if a == 255:
                print('Tu es un être, tes paroles sont un flag')
            else:
                print('Néant tu es, Néant tu resteras')

    return core

@block
def Silicon(Flag_in):
    undeuxtroisetplusencore = Signal(modbv(0, 0, 16))
    little_box = Signal(bool(0))
    little_bigger_box = Signal(modbv(0, 0, 256))
    tic_tac_toe = Signal(bool(0))

    go_in = [Signal(bool(0)) for _ in range(8)]

    Block0_inst = Block0(Flag_in[0], go_in[0])
    Block1_inst = Block1(Flag_in[1], go_in[1])
    Block2_inst = Block2(Flag_in[2], go_in[2])
    Block3_inst = Block3(Flag_in[3], go_in[3])
    Block4_inst = Block4(Flag_in[4], go_in[4])
    Block5_inst = Block5(Flag_in[5], go_in[5])
    Block6_inst = Block6(Flag_in[6], go_in[6])
    Block7_inst = Block7(Flag_in[7], go_in[7])

    Tulipe_inst = Tulipe(go_in, little_box, undeuxtroisetplusencore)
    plic_ploc_inst = plic_ploc(little_box, little_bigger_box, undeuxtroisetplusencore, tic_tac_toe)
    time_to_see_inst = time_to_see(little_bigger_box, undeuxtroisetplusencore, tic_tac_toe)
    go_up_go_up_GO_UP_inst = go_up_go_up_GO_UP(undeuxtroisetplusencore, tic_tac_toe)

    @always(delay(10))
    def tic_tac_toe_generator():
        tic_tac_toe.next = not tic_tac_toe

    return Tulipe_inst, plic_ploc_inst, time_to_see_inst, go_up_go_up_GO_UP_inst, tic_tac_toe_generator, Block7_inst, Block6_inst, Block5_inst, Block4_inst, Block2_inst, Block3_inst, Block0_inst, Block1_inst

attempt = input('Certains de mes amis sont des Etres et d\'autre des Néants.\n'
               'Pour le vérifier j\'ai mis au point un circuit électronique!\n'
               'Partage lui un peu de ta sagesse pour que nous puissions savoir ce que tu es!\n')

bus = [modbv(0, 0, 2 ** 17) for _ in range(8)]
if len(attempt) == 17:
    x = 0
    for l in attempt:
        letter = modbv(ord(l), 0, 2 ** 8)
        for i in range(8):
            bus[i] += letter[i] * 2 ** x
        x += 1

simInst = Silicon([Signal(line) for line in bus])
simInst.run_sim(170)

The validation logic is performed in the time_to_see function. On each rising clock edge, the result of block i is stored in bit i of the little_bigger_box signal. The time_to_see function then checks that little_bigger_box is 255, i.e. that each bit is set to 1.

Solving this challenge involves solving the equations corresponding to each of the blocks. To me this looks like a classical example of the boolean satisfiability problem. I should use used a solver during the CTF but but I didn’t know one at the time, instead I used bruteforce because it was possible: state ~ 2^17.

First I made some classes to represent boolean operations:

import sys

counter = 0
class Leaf:
  def __init__(self, name = None):
    global counter
    if not name:
      self.name = name or f"x_{counter}"
      counter += 1

    self.type = "leaf"
    self.value = None

  def __repr__(self):
    if not self.value is None:
      return f"{self.name}={self.value}"
    return self.name

  def compute(self, reset):
    return self.value

class NegNode:
  def __init__(self, operand):
    self.type = "unary"
    self.operand = operand
    self.value = None

  def compute(self, reset = False):
    if reset: self.value = None
    if self.value: return
    self.operand.compute(reset)
    if self.operand.value is None: return
    self.value = not self.operand.value

  def __repr__(self):
    return f"!({self.operand})"


class BinaryNode:
  def __init__(self, op, *operands):
    self.type = "binary"
    self.operands = operands
    self.op = op
    self.value = None

  def compute(self, reset = False):
    if reset: self.value = None
    if self.value: return
    self.operands[0].compute(reset)
    if self.operands[0].value is None: return
    self.operands[1].compute(reset)
    if self.operands[1].value is None: return

    if self.op == "xor":
      self.value = self.operands[0].value ^ self.operands[1].value
    elif self.op == "and":
      self.value = self.operands[0].value & self.operands[1].value
    elif self.op == "or":
      self.value = self.operands[0].value | self.operands[1].value
    else:
      raise BaseException(f"Unknown operator {self.op}")

  def __repr__(self):
    return f"({self.operands[0]} {self.op} {self.operands[1]})"


def XOR(a, b, t = None):
  return BinaryNode("xor", a, b)

def OR(a, b, t = None):
  return BinaryNode("or", a, b)

def AND(a, b, t = None):
  return BinaryNode("and", a, b)

def NOT(a, t = None):
  return NegNode(a)

And then the code the brute force the solution to each block and recreate the input string:

blocks = [block0, block1, block2, block3, block4, block5, block6, block7]
keys = []
for block_i in range(8):
  mask = (1 << 18) - 1
  block = blocks[block_i]
  node = block()
  found = False
  print(f"Block{block_i}:")
  for i in range(1 << 17):
    print(f"\riteration {i}/{1 << 17}", end="")
    for j in range(17):
      b[j].value = (i & (1 << j)) >> j

    node.compute(True)
    # print(t[85])
    if node.value:
      print("\nsatisfied by", i)
      keys.append(i)
      found = True

    if found: break
    else:
      raise BaseException("Cannot find a solution")


print(keys) # [85137, 71688, 111538, 66570, 126876, 131070, 39435]
for i in range(17):
  letter = 0
  for k in range(8):
    letter += ((keys[k] & (1 << i)) >> i) << k

  print(chr(letter), end="")

And the flag was really about boolean satisfiability: 404CTF{Al0r5, 54t1sf41t?}.