404CTF Writeup - Reverse Engineering
Le Divin CrackMe
In this introduction to reverse engineering, we need to find three pieces of information about an executable given to us. We need to find the compiler, the function used to check the password and the password itself.
For the compiler part, we use objdump to disassemble to binary and read the .comment section:
objdump -s --section .comment divin-crackme
# divin-crackme: file format elf64-x86-64
#
# Contents of section .comment:
# 0000 4743433a 20284465 6269616e 2031322e GCC: (Debian 12.
# 0010 322e302d 31342920 31322e32 2e3000 2.0-14) 12.2.0.The next step is to open up a decompiler (or a disassembler if you’re bold enough) and start analyzing the program. I opened up ghidra and it has already done most of the work for us:

As you can see, the password is compared against chunk of the passwords using the strncmp function.
Then it’s a matter of concatenation to see that the flag is: 404CTF{gcc:strncmp:L4_pH1l0soPh13_d4N5_l3_Cr4cKm3}
L’inspiration en images
We are given a program that shows a painting with a light cone effect. The goal of the challenge is the find a the “hidden background”. The flag will be in the format 404CTF{vec4(r,g,b,a)}.

The flag format is already very revealing and we can confirm this hypothesis when we decompile the program using ghidra.
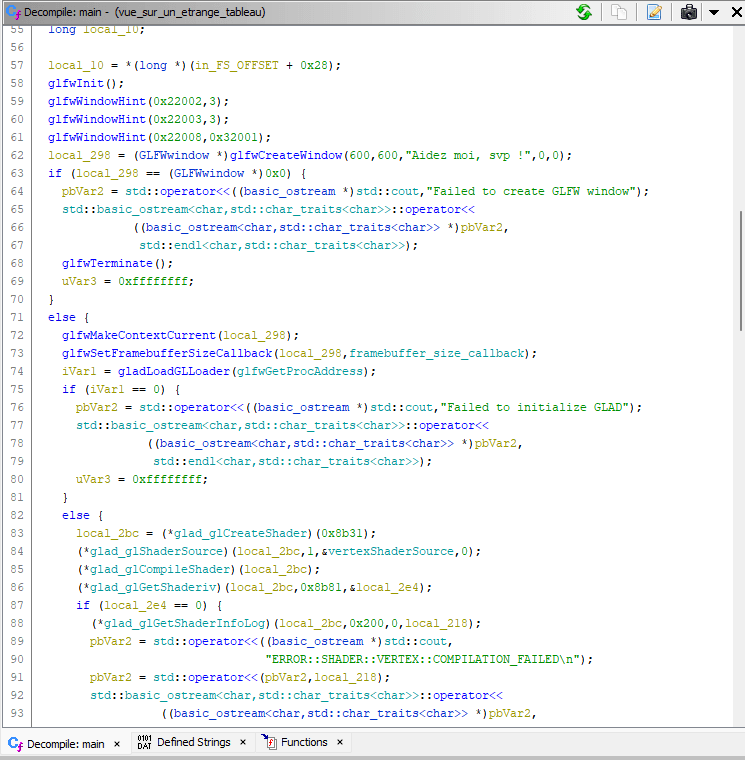
As you can see, the program is using the C++ and glfw which is a lightweight utility library for use with OpenGL (Open Graphics Library). Although diving into the disassembly might be tempting, it’s not directly related to finding the flag. Instead, let’s focus on the main loop of the program:

- Check for Program Close: The program checks if the close button has been requested. If so, it terminates.
- User Input Handling: The main loop handles user input, particularly mouse movements in this case.
- Frame Clearing: The frame is cleared to prepare for the next rendering.
- Shader Program Setup: The program sets up the shader, updating resolution and mouse position (uniform inputs to the shader).
- Texture Binding: A texture, depicting a black background with scribbles, is bound (what we see when using the app).
- Drawing: The program draws everything, applying the light cone effect and any overrides.
- Window Events Processing: The loop processes window events.
In the process, the only “background” that has been overriden is the background used when clearing the frame. In the disassembly it’s this line
(*glad_glClearColor)(0x3e4ccccd,0x3e99999a,0x3e99999a,0x3f800000);
# The OpenGL spec says that this function has the following signature
void glClearColor(
GLfloat red,
GLfloat green,
GLfloat blue,
GLfloat alpha
);It’s very likely that GLfloat = float, so we can use a float decoder online to get the values of color channels.
Doing so will reveal that the flag is: 404CTF{vec4(0.2, 0.3, 0.3, 1.0)}.
Encore une mise à jour
This is a python 3.11 reverse engineering challenge based on the bytecode specialization introduced in this version. Here is the script:
# /!\ Ce challenge est conçu pour PYTHON 3.11 !
# Il ne FONCTIONNERA PAS SUR UNE VERSION ANTERIEURE !
# Il a été testé, et est fonctionnel sur python 3.11.0 et python 3.11.3, je ne garanti RIEN, sur les autres versions
# Modifiez le fichier à vos risques et périls.... Je ne suis pas responsable.
h = __import__('dis')
dico = {'adaptive': True}
a = input('Mot de passe : ')
a = [ord(c) for c in a]
def check(dumas, zola):
cody = h.Bytecode(check, **dico).dis().count('I')
carmen = 0
if dumas[36] + cody * dumas[37] + dumas[38] == 25556:
carmen += 1
if dumas[3] + cody * dumas[4] + dumas[5] == 19862:
carmen += 1
if dumas[21] + cody * dumas[22] + dumas[23] == 39570:
carmen += 1
if dumas[0] + dumas[1] + cody * dumas[2] == 35329:
carmen += 1
if dumas[6] + dumas[7] + cody * dumas[8] == 67347:
carmen += 1
if dumas[3] + dumas[4] + cody * dumas[5] == 100914:
carmen += 1
if dumas[3] + cody * dumas[4] + dumas[5] == 49274:
carmen += 1
if dumas[6] + cody * dumas[7] + dumas[8] == 61221:
carmen += 1
if dumas[36] + dumas[37] + cody * dumas[38] == 64773:
carmen += 1
if dumas[9] + dumas[10] + cody * dumas[11] == 49360:
carmen += 1
if dumas[9] + cody * dumas[10] + dumas[11] == 18857:
carmen += 1
if dumas[9] + cody * dumas[10] + dumas[11] == 46721:
carmen += 1
if dumas[15] + dumas[16] + cody * dumas[17] == 58164:
carmen += 1
if dumas[15] + dumas[16] + cody * dumas[17] == 144852:
carmen += 1
if dumas[12] + dumas[13] + cody * dumas[14] == 147438:
carmen += 1
if dumas[12] + dumas[13] + cody * dumas[14] == 59202:
carmen += 1
if dumas[45] + cody * dumas[46] + dumas[47] == 39501:
carmen += 1
if dumas[12] + cody * dumas[13] + dumas[14] == 25080:
carmen += 1
if dumas[15] + cody * dumas[16] + dumas[17] == 27661:
carmen += 1
if dumas[18] + dumas[19] + cody * dumas[20] == 135810:
carmen += 1
if dumas[18] + cody * dumas[19] + dumas[20] == 128064:
carmen += 1
if dumas[15] + cody * dumas[16] + dumas[17] == 68683:
carmen += 1
if dumas[12] + cody * dumas[13] + dumas[14] == 62232:
carmen += 1
if dumas[24] + cody * dumas[25] + dumas[26] == 66114:
carmen += 1
if dumas[27] + cody * dumas[28] + dumas[29] == 25071:
carmen += 1
if dumas[6] + cody * dumas[7] + dumas[8] == 152553:
carmen += 1
if dumas[6] + dumas[7] + cody * dumas[8] == 27099:
carmen += 1
if dumas[21] + dumas[22] + cody * dumas[23] == 54563:
carmen += 1
if dumas[45] + cody * dumas[46] + dumas[47] == 98325:
carmen += 1
if dumas[39] + dumas[40] + cody * dumas[41] == 115125:
carmen += 1
if dumas[24] + cody * dumas[25] + dumas[26] == 26640:
carmen += 1
if dumas[21] + dumas[22] + cody * dumas[23] == 135833:
carmen += 1
if dumas[9] + dumas[10] + cody * dumas[11] == 122890:
carmen += 1
if dumas[39] + dumas[40] + cody * dumas[41] == 46239:
carmen += 1
if dumas[0] + dumas[1] + cody * dumas[2] == 87961:
carmen += 1
if dumas[27] + dumas[28] + cody * dumas[29] == 144847:
carmen += 1
if dumas[30] + dumas[31] + cody * dumas[32] == 35402:
carmen += 1
if dumas[27] + dumas[28] + cody * dumas[29] == 58159:
carmen += 1
if dumas[3] + dumas[4] + cody * dumas[5] == 40542:
carmen += 1
if dumas[0] + cody * dumas[1] + dumas[2] == 42776:
carmen += 1
if dumas[30] + cody * dumas[31] + dumas[32] == 57633:
carmen += 1
if dumas[42] + cody * dumas[43] + dumas[44] == 26019:
carmen += 1
if dumas[18] + dumas[19] + cody * dumas[20] == 54540:
carmen += 1
if dumas[18] + cody * dumas[19] + dumas[20] == 51438:
carmen += 1
if dumas[21] + cody * dumas[22] + dumas[23] == 98394:
carmen += 1
if dumas[24] + dumas[25] + cody * dumas[26] == 51973:
carmen += 1
if dumas[24] + dumas[25] + cody * dumas[26] == 129373:
carmen += 1
if dumas[30] + dumas[31] + cody * dumas[32] == 88034:
carmen += 1
if dumas[0] + cody * dumas[1] + dumas[2] == 17234:
carmen += 1
if dumas[30] + cody * dumas[31] + dumas[32] == 143547:
carmen += 1
if dumas[33] + cody * dumas[34] + dumas[35] == 43078:
carmen += 1
if dumas[33] + dumas[34] + cody * dumas[35] == 42770:
carmen += 1
if dumas[33] + cody * dumas[34] + dumas[35] == 107320:
carmen += 1
if dumas[36] + dumas[37] + cody * dumas[38] == 26073:
carmen += 1
if dumas[33] + dumas[34] + cody * dumas[35] == 17228:
carmen += 1
if dumas[39] + cody * dumas[40] + dumas[41] == 27627:
carmen += 1
if dumas[39] + cody * dumas[40] + dumas[41] == 68649:
carmen += 1
if dumas[27] + cody * dumas[28] + dumas[29] == 62223:
carmen += 1
if dumas[42] + cody * dumas[43] + dumas[44] == 64719:
carmen += 1
if dumas[45] + dumas[46] + cody * dumas[47] == 29161:
carmen += 1
if dumas[42] + dumas[43] + cody * dumas[44] == 35842:
carmen += 1
if dumas[36] + cody * dumas[37] + dumas[38] == 63482:
carmen += 1
if dumas[42] + dumas[43] + cody * dumas[44] == 89248:
carmen += 1
if dumas[45] + dumas[46] + cody * dumas[47] == 72505:
carmen += 1
zola+zola
return carmen == 32
if len(a) != 48:
print('Non, c\'est pas ça...')
exit(0)
for i in range(10): #Checker 10 fois c'est mieux que 1 seule fois ! Comme ça je suis sûr de moi...
if not (check(a, 1) or check(a, 1)):
print('Non, c\'est pas ça...')
exit(0)
print('Bravo ! Le flag est 404CTF{le mot de passe que vous avez rentré pour valider}!')We are a system of 64 equations on the triplets {dumas[i], dumas[i+1], dumas[i+2]} of letters of the flag. Analyzing the equations more carefully we notice that:
- For each
0 <= i < 16, 4 equations exists For exampledumas[0] + dumas[1] + cody * dumas[2] == 35329dumas[0] + dumas[1] + cody * dumas[2] == 87961dumas[0] + cody * dumas[1] + dumas[2] == 42776dumas[0] + cody * dumas[1] + dumas[2] == 17234
- These equations come in 2 types based on the position of the factor
cody:- type 1:
dumas[i] + cody *dumas[i+1] + dumas[i+2] == rhs - type 2:
dumas[i] + dumas[i+1] + cody *dumas[i+2] == rhs
- type 1:
- There are exactly 2 type 1 and 2 type 2 equations
- type 1:
dumas[0] + dumas[1] + cody * dumas[2] == 35329dumas[0] + dumas[1] + cody * dumas[2] == 87961
- type 2:
dumas[0] + cody * dumas[1] + dumas[2] == 42776dumas[0] + cody * dumas[1] + dumas[2] == 17234
- type 1:
- Each of these equations have a different right-hand-sides
This means that for a given
iand a specific value ofcody, only one type 1 and only one type 2 can be satisfied for any assignement. At maximum, we can only satisfy 32 of these equations, which is the value we need to pass thecheckfunction.
With this conclusion we can bruteforce some solutions after knowing the value of cody. I actually did this during the CTF and found only one solution in printable characters which was in fact the flag. But let’s continue entertaining these thoughts to find a faster method.
The Python Interpreter’s Optimization
While it seems like we can find many flag solutions (not only 1) because that there is only 32 active constraints, this isn’t necessarily true. The check function is run many (20) times, The python interpreter will specialize bytecode instructions in order to optimize for speed, This in turn will changes the value of cody, adding more constraints (64 to be precise) on the values of dumas to produce a unique flag for this challenge.
Working with printable characters
If we assume that the flag consists only of the printable characters (a very reasonable assumption), then:
33 <= dumas[i], dumas[i+1], dumas[i+2] <= 126:dumas[i+1] = (rhs - dumas[i] - dumas[i+2]) / codyfor type 1 equationsdumas[i+2] = (rhs - dumas[i] - dumas[i+1]) / codyfor type 2 equations
For any of these: (rhs - 252) / 518 <= dumas[i+1], dumas[i+2] <= (rhs - 66) / 518.
The values of cody happen to be are large enough to uniquely compute dumas[i+1] and dumas[i+2]. This doesn’t mean what the solutions we get by solving these inequalities are characters of the flag, but characters of the flag are definitely among the solutions.
A character of the flag verifies the property that it is found using the 2 equations of the same type and the 2 different values cody (earlier conclusion) so we will require this.
Here is the summary for this solution:
- Get the 2 possible values of
cody - For each
i, solvedumas[i+1]anddumas[i+2]from the previous inequalities, and deducedumas[i] - Concatenate to get the flag
Getting the possible values of cody
Given the values of cody:
We can’t simply add print(cody) inside the check function because that will modify it’s bytecode and change cody. But we can do it outside, I redefined h.Bytecode.dis to print count('I') (the value which will be assigned to cody) before returning the disassembly object.
original_dis = h.Bytecode.dis
def new_dis(self):
ret = original_dis(self)
print('>', ret.count('I'))
return ret
h.Bytecode.dis = new_disFinding an assignement
import math
from itertools import product
def is_printable(d):
return d >= 33 and d <= 126
# Find a the unique `d` that verifies the equation with right hand side `rhs` and `cody`
# type 1 => d = dumas[i+1]
# type 2 => d = dumas[i+2]
# `d` might not be part of the flag though, because we don't garentee that it will solve the other same type equation for the other cody
# this step is the accomplished by the next function `solve`
def find_d(rhs, cody):
interval = [(rhs - 252) / cody, (rhs - 66) / cody]
d = math.ceil(interval[0])
is_sat = d == math.floor(interval[1]) and is_printable(d)
return is_sat, d
def solve(equations, codies):
for equation_i, cody_i in product(range(2), range(2)):
sat, d = find_d(equations[equation_i], codies[cody_i])
if not sat: continue #searching
other_sat, other_d = find_d(equations[1 - equation_i], codies[1 - cody_i])
if other_sat and d == other_d:
return True, d
else:
print("ignoring false solution", d1)
return False, None
# Extracted from the challenge program
# entries are ordered by `i`, representing equations with the variables {dumas[i], dumas[i+1], dumas[i+2]}
# each entry consists of 2 tuples, the first tuple contains the right hand side values of the type 1 equations
# same logic for the second tuple
equations = [
[(42776, 17234), (35329, 87961)],
[(19862, 49274), (100914, 40542)],
[(61221, 152553), (67347, 27099)],
[(46721, 18857), (49360, 122890)],
[(25080, 62232), (147438, 59202)],
[(27661, 68683), (58164, 144852)],
[(128064, 51438), (135810, 54540)],
[(39570, 98394), (54563, 135833)],
[(66114, 26640), (51973, 129373)],
[(25071, 62223), (144847, 58159)],
[(57633, 143547), (35402, 88034)],
[(43078, 107320), (42770, 17228)],
[(25556, 63482), (64773, 26073)],
[(27627, 68649), (115125, 46239)],
[(26019, 64719), (35842, 89248)],
[(39501, 98325), (29161, 72505)]
];
codies = [518, 1292]
flag = ""
for entry in equations:
type1, type2 = entry
d1_sat, d1 = solve(type1, codies)
d2_sat, d2 = solve(type2, codies)
if not d1_sat or not d2_sat: raise BaseException("cannot find the flag")
# We don't know which cody will satisfy this equation, but we know that one of them will
d0 = type1[0] - codies[0]*d1 - d2
if not is_printable(d0): d0 = type1[0] - codies[1]*d1 - d2
flag += chr(d0) + chr(d1) + chr(d2)
print(flag)If you run this script, you will find the flag: 404CTF{H!Dd&N-v4r$_f0r_5p3ciaLiz3d_0pCoD3S!|12T5Y22EML8}
This method is really fast for finding the unique flag but it’s not general (issues include: 2 doubles, lack of actual constraint satisfaction, etc..) I think we can improve it to find all the flags if there are many and report failures more precisely. But in another blog post if you ask for it.
Introspection
In this challenge, we are given an elf program asking for a password: the password being the flag. Since it is an easy challenge, I tried running strings against it hoping for an easy solve but I found nothing meaningful.
The next step is to decompile to program and see what is going on. And boy, it was really introspective. I’m not going to go much into detail, but the program basically unpacks a part of itself to create a new executable program and loads it into a temporary file created using the memfd_create system call (you can lookup the system call numbers to identify it, ghidra didn’t compile this correctly for me).
I tried doing this manually and I went up to 10 iterations but it just keeps going. Since I already have 10 samples, I identified a pattern in the next program and next key positions and I used python to automate the unpacking process for me. From there, I kept increasing this number of iterations until I got an error.
Here is a script that unpacks the program a 101 times.
import sys
from elftools.elf.elffile import ELFFile
def align_address(address, n = 16):
aligned_address = (address) & ~(n - 1)
return aligned_address
PROGRAMS = [
[0x4060, 0x4060 + 0x18AE68],
# [0x4060, 0x4060 + 0x186E68],
# [0x4060, 0x4060 + 0x182FC0],
# [0x4060, 0x4060 + 0x17F1C8],
# [0x4060, 0x4060 + 0x17B330],
# [0x4060, 0x4060 + 0x177460],
# [0x4060, 0x4060 + 0x173658],
# [0x4060, 0x4060 + 0x16F928],
# [0x4060, 0x4060 + 0x16BAE0],
# [0x4060, 0x4060 + 0x167BA8],
# [0x4060, 0x4060 + 0x163CA8]
]
KEYS = [
[0x18eee0, 0x18eee0 + 0x41C],
# [0x18aee0, 0x18aee0 + 0x712],
# [0x187040, 0x187040 + 0x5B1],
# [0x183240, 0x183240 + 0x50F],
# [0x17f3a0, 0x17f3a0 + 0x5B1],
# [0x17b4e0, 0x17b4e0 + 0x5DA],
# [0x1776c0, 0x1776c0 + 0x52A],
# [0x1739a0, 0x1739a0 + 0x441],
# [0x16fb60, 0x16fb60 + 0x553],
# [0x16bc20, 0x16bc20 + 0x64D],
# [0x167d20, 0x167d20 + 0x614]
]
def get_next_iteration_parameters(iteration):
with open('./introspection_' + str(iteration), 'rb') as f:
elf = ELFFile(f)
greatest_segment, greatest_segment_size = None, 0
for segment in elf.iter_segments():
segment_start = segment.header.p_vaddr
segment_size = segment.header.p_filesz
segment_end = segment_start + segment_size
if segment_size > greatest_segment_size:
greatest_segment = segment
greatest_segment_size = segment_size
start = greatest_segment.header.p_vaddr
data = greatest_segment.data()
if iteration == 0:
print("Saved parameters for iteration 0")
key = data[KEYS[0][0] - start: KEYS[0][1] - start]
program = data[PROGRAMS[0][0] - start: PROGRAMS[0][1] - start]
return key, program
print("Found greatest segment", hex(start), hex(start + greatest_segment_size))
data = greatest_segment.data()
expected_key_size_position = align_address(greatest_segment_size - 4, 4)
print("Expected key size position", hex(expected_key_size_position))
key_size = int.from_bytes(data[expected_key_size_position:expected_key_size_position+4], "little")
print(key_size)
print("Expected key size", hex(key_size))
expected_key_position = align_address(expected_key_size_position - key_size)
print("Expected key position:", hex(expected_key_position))
key = data[expected_key_position:expected_key_position + key_size]
head = expected_key_position - 1
# A bunch of zeros until we find the program size
while not data[head]:
head -= 1
expected_program_size_position = align_address(head, 8)
print("Expected program size", hex(expected_key_size_position))
program_size = int.from_bytes(data[expected_program_size_position:expected_program_size_position+8], "little")
print("Expected program size", hex(program_size))
expected_program_position = expected_program_size_position - program_size
print("Expected program position", hex(expected_program_position))
program = data[expected_program_position:expected_program_position + program_size]
print("Key sample", key[:4], key[-4:])
print("Program sample", program[:4], program[-4:])
print("len(key) =", hex(len(key)))
return key, program
def next_iteration(iteration):
key, program = get_next_iteration_parameters(iteration)
print("Unpacking ELF...")
program_size = len(program)
key_size = len(key)
correct_program = [0] * program_size
for i in range(program_size):
if i % 10240 == 0 or i == program_size-1:
print(f"\r {i}/{program_size} bytes processed", end="")
sys.stdout.flush()
correct_program[i] = (-1 + key[i % key_size] + 1^program[i]) & 0xff
correct_program = bytes(correct_program)
print("\nDone ! Saving file...")
with open(f'./introspection_{iteration+1}', 'wb') as f:
f.write(correct_program)
for i in range(0, 101):
next_iteration(i)I think there are some aspects of the program that I haven’t yet understood, like maybe predicting the next parameters is actually easier than what I’ve used in the end. If you know a better method please let me know.
In any case, you can run the script like this:
cp introspection introspection_0
python3 unpack_101.py
strings introspection_101
rm introspection_*Analyzing the output of strings, you’ll find the flag: 404CTF{5t3althy_f1Le$-4nD_aUt0matIon}